Can All Matrices Be Reduced To Reduced Row Echelon Form In reduced row echelon form a matrix must satisfy the following properties If there is any rows containing all zeros they should be at the bottom of the matrix Example 1 begin bmatrix 1 0 0 0 1 0 0 0 0
It s easy to show that any 2 2 2 2 matrix can be in row reduced echelon form Now assume that for n N n N we have that n 1 n 1 n 1 n 1 matrices can be in row reduced As we have seen in earlier sections we know that every matrix can be brought into reduced row echelon form by a sequence of elementary row operations Here we will prove that the resulting matrix is unique in other words the resulting
Can All Matrices Be Reduced To Reduced Row Echelon Form
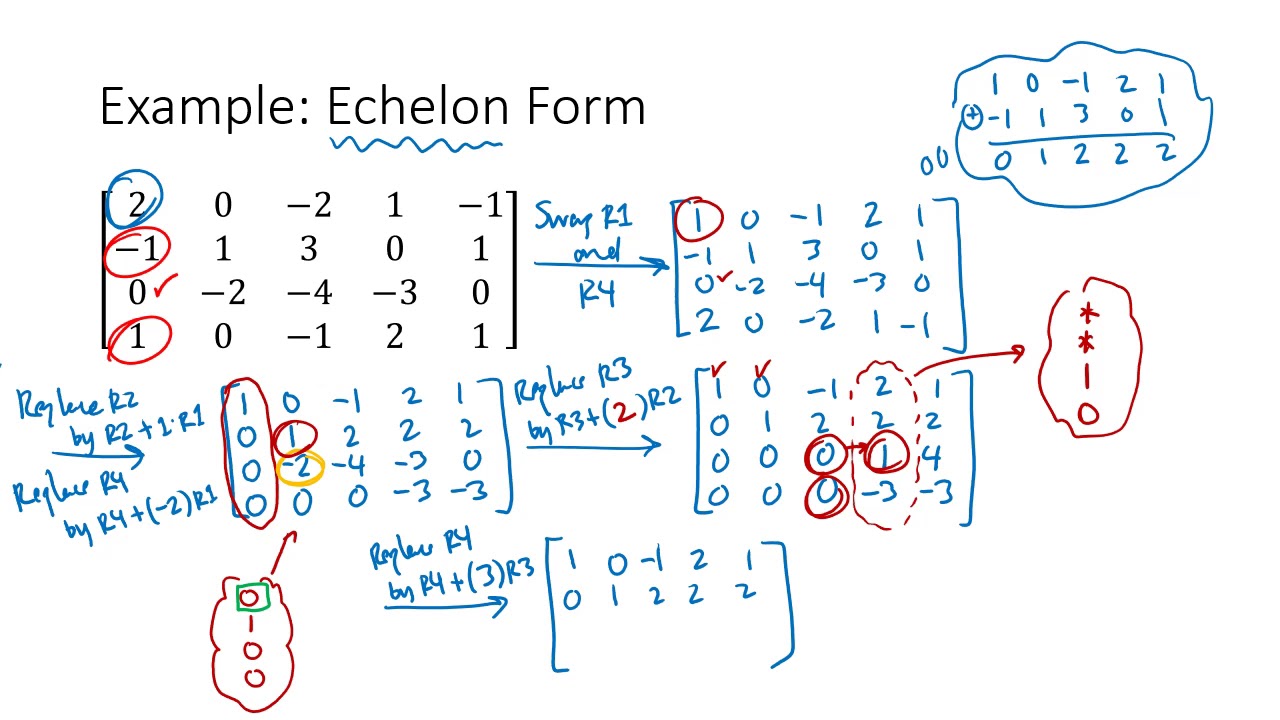
Can All Matrices Be Reduced To Reduced Row Echelon Form
https://i.ytimg.com/vi/72ysuwtYA0c/maxresdefault.jpg
Reduced Row Echelon Form YouTube
https://i.ytimg.com/vi/7bxGuzUMYsY/maxresdefault.jpg
Augmented Matrices Row Echelon Form YouTube
https://i.ytimg.com/vi/BWBckWPjfpw/maxresdefault.jpg
Learning Objectives Learn to perform row operations to transform a matrix into echelon form or reduced echelon form Identify pivot columns of a matrix Use technology to perform row Row Echelon Form REF and Reduced Row Echelon Form RREF are essential for simplifying matrices to solve linear equations with specific properties governing their structure
If A is an invertible square matrix then rref A I Instead of Gaussian elimination and back substitution a system of equations can be solved by bringing a matrix to reduced row echelon Every matrix is row equivalent to one and only one matrix in reduced row echelon form We ll give an algorithm called row reduction or Gaussian elimination which demonstrates that every
More picture related to Can All Matrices Be Reduced To Reduced Row Echelon Form
What Is Row Echelon Form YouTube
https://i.ytimg.com/vi/zksRGHYD76g/maxresdefault.jpg?sqp=-oaymwEmCIAKENAF8quKqQMa8AEB-AH-CYAC0AWKAgwIABABGGUgZShlMA8=&rs=AOn4CLB0KiIYxwlzd_IjqeAFz5lmgNag7A
Reduced Row echelon Form YouTube
https://i.ytimg.com/vi/rgK-hhXGfus/maxresdefault.jpg
Linear Algebra Example Problems Reduced Row Echelon Form YouTube
https://i.ytimg.com/vi/KFSkWm47Trs/maxresdefault.jpg
If a matrix in echelon form satisfies the following additional conditions then it is in reduced echelon form or reduced row echelon form The leading entry in each non zero row is 1 We will give an algorithm called row reduction or Gaussian elimination which demonstrates that every matrix is row equivalent to at least one matrix in reduced row echelon
If a matrix A is row equivalent to an echelon matrix U we call U an echelon form or row echelon form of A if U is in reduced echelon form we call U the reduced echelon form of A Chapter 1 Section III covers reduced echelon form In an echelon form matrix any all zero row is at the bottom and for rows that are not all zero after the first row the leading entry in that
Matrices Reduced Row Echelon Form 1 Vectors And Spaces Linear
https://i.ytimg.com/vi/L0CmbneYETs/maxresdefault.jpg
Finding The Solution To A Matrix In Reduced Row Echelon Form YouTube
https://i.ytimg.com/vi/HrKKezSjnAs/maxresdefault.jpg
https://www.geeksforgeeks.org › reduced-row-echelon-f…
In reduced row echelon form a matrix must satisfy the following properties If there is any rows containing all zeros they should be at the bottom of the matrix Example 1 begin bmatrix 1 0 0 0 1 0 0 0 0
https://math.stackexchange.com › questions › ...
It s easy to show that any 2 2 2 2 matrix can be in row reduced echelon form Now assume that for n N n N we have that n 1 n 1 n 1 n 1 matrices can be in row reduced
Using Reduced Row Echelon Form To Solve A System Of Equations YouTube
Matrices Reduced Row Echelon Form 1 Vectors And Spaces Linear
Ex Write A 3x3 Matrix In Reduced Row Echelon Form Identity YouTube
01 7 Row Equivalence Of Matrices YouTube
Row Echelon Form Vs Reduced Row Echelon Form YouTube
Ex 1 Solve A System Of Two Equations With Using An Augmented Matrix
Ex 1 Solve A System Of Two Equations With Using An Augmented Matrix
Ex 2 Solve A System Of Two Equations Using An Augmented Matrix
How To Check Echelon And Reduced Echelon Form Of Metrices Linear
Parametric Form Solution Of Augmented Matrix In Reduced Row Echelon
Can All Matrices Be Reduced To Reduced Row Echelon Form - A system of linear equations can be solved by reducing its augmented matrix into reduced echelon form A matrix can be changed to its reduced row echelon form or row
